Сетевой график, пример построения

Как выглядит график

Любой привычный нам график представлен кривой, расположенной на плоскости (реже в пространстве). Но вид сетевого плана существенно отличается.

Сетевой график проекта может выглядеть двояко: одна методика предполагает обозначение операций в узлах блок-схемы (ОУ), вторая использует для этого соединительные стрелки (ОС). Гораздо удобнее использовать первый способ.

Операция обозначается круглым или прямоугольным блоком. Стрелки, их соединяющие, определяют взаимосвязи между действиями. Поскольку названия работ могут быть достаточно длинными и объемными, в блоках проставляют номера операций, а к графику составляется спецификация.

Графики

Графики разные по строительству скачать :

Примеры графиков производства работ:

1 График производства земляных работ, пример скачать jpg, скачать rar

2 График производства работ по строительству школы, пример скачать doc

3 График производства работ по объекту: Центральный тепловой пункт ЦТП, пример скачать xls, скачать zip

4 График производства работ на комплекс работ по устройству наружного освещения, кабельной сети и декоративной подсветки, пример скачать xls, скачать zip

5 График производства работ на реконструкцию, пример скачать xls, скачать zip

Примеры календарных графиков:

1 Календарный график производства работ, календарный график движения рабочей силы, машин и механизмов на прокладку полиэтиленовых труб, бланк (в формате Компас V15.1) скачать frw

2 Календарный график выполнения работ по объекту, пример скачать xls.

3 Календарный график, пример скачать zip, скачать pdf.

4 Календарный план производства работ на тепловые сети, пример скачать zip, скачать doc.

5 Календарный план производства работ на установку опор ВОЛС, пример скачать zip, скачать doc.

6 Месячно-суточный график выполнения работ, пример скачать xls, скачать zip

Примеры прочих графиков:

1 График подготовки и сдачи исполнительной технической документации ИТД, пример скачать xls, скачать zip

2 График потребности в рабочих кадрах и основных строительных машинах, пример скачать xls, скачать zip

3 График поступления на объект строительных конструкций, изделий и материалов, пример скачать xls, скачать zip

4 График поставок материалов и оборудования, пример скачать doc, скачать zip

5 График движения рабочей силы, пример скачать xls, скачать zip

5а График движения персонала на строительстве, пример скачать xls, скачать zip

6 График выполнения СМР, пример скачать pdf, скачать zip

7 График кирпичной кладки, пример скачать xls, скачать zip

8 Плановый график расстановки специалистов подрядной организации, пример скачать xls, скачать zip

9 Фактический график расстановки специалистов подрядной организации, пример скачать xls, скачать zip

10 График (табель) учёта фактически отработанных дней специалистов подрядной организации, пример скачать xls+приложение, скачать zip

11 План график технического обслуживания сети газопотребления, пример скачать pdf, скачать zip

Вернуться к разделу: «Акты, схемы протокола и прочее».

Смотрите состав исполнительной в разделе: «Состав исполнительной»

Скачивайте акты, протокола и другое в разделе: «Акты и прочее»

Скачивайте полезные книги, ГОСТы, СнИПы в разделе: «ГОСТы и книги

Корректировка сетевой модели

Корректировка сетевой модели может проводиться и в первом случае, если имеется возможность для повышения эффективности реализации запланированных операций.

В сетевом планировании выделяют три способа корректировки модели:

1. изменение сроков выполнения критических операций за счет привлечения дополнительных ресурсов, в качестве которых могут выступать денежные средства, материалы или человеческие ресурсы;
2. изменение сроков выполнения критических операций за счет привлечения исполнителей, занятых на других операциях, при сохранении изначальных параметров ресурсов;
3. изменение сроков выполнения операций за счет совмещения их выполнения.

В первом случае корректировка сетевой модели осуществляется без изменения сетевой диаграммы. Данный подход чаще всего практикуется в тех случаях, когда для выполнения операций остаются свободные ресурсы, не задействованные в других операциях.

Во втором случае сетевая диаграмма также остается неизменной. Данный подход используется в тех случаях, когда возможно увеличить срок выполнения операций, не принадлежащих к критическому пути.

Третий случай применяется при невозможности использования дополнительных ресурсов и подразумевает повторное построение сетевой диаграммы.

После проведения корректировки осуществляется построение альтернативной сетевой модели.

Следует отметить, что в корректировке сетевой модели заключается фундаментальное назначение сетевого планирования. Благодаря построению сетевых моделей уже на ранней стадии планирования могут быть выявлены условия, свидетельствующие о том, что в заданные директивные сроки проект невозможно будет выполнить. Поэтому для получения приемлемых с точки зрения целей проекта сроков возможно осуществление коррекции расписания операций по принципу изменения продолжительности критических операций. Таким образом, если проект или заданный план действий не укладывается в директивные сроки, то предпринимается попытка сократить сроки выполнения критических операций за счет изменения их зависимости от первоначально заданных параметров их выполнения.

Литература

1. Черняк В.З., Довдиенко И.В. Методы принятия управленческих решений. – М.: Академия, 2013.
2. Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г., Полковников А.В. Управление проектами. – М.: Омега-Л, 2012.
3. Новыш Б.В., Шешолко В.К., Шаститко Д.В. Экономико-математические методы принятия решений. – М.: Инфра-М, 2013.
4. Урубков А.Р., Федотов И.В. Методы и модели оптимизации управленческих решений. – М.: изд-во АНХ, 2011.
5. Сухачев К.А., Колосова Е.С. Практика применения технологий календарно-сетевого планирования. // Нефтегазовая вертикаль. – 2010. – №11 (240), июнь 2010. – С. 28-30.

Базовый алгоритм и виды связей сетевого графика

Сетевой график позволяет увидеть структуру работ, представить все этапы и взаимосвязи с требуемой степенью детализации. На его основе производится разработка обоснованного плана мероприятий с учетом более эффективного использования ресурсов по заданным критериям. Диаграмма позволяет производить поливариантный анализ альтернативных решений для улучшения календарного плана с использованием компьютерных технологий. Вспомним основные правила построения сетевой модели метода «вершина – работа».

1. Элементы сетевого графика включают работы и зависимости (связи) между ними. События на графике не отражаются за исключением вех, представляющих собой основные наиболее важные события, изображаемых в форме «ромбиков», работ с нулевой продолжительностью.
2. Работа представляет собой неделимый элемент процесса, требующий времени и других ресурсов для выполнения, изображается в виде прямоугольника, вытянутого по горизонтали. Исходя из этого правила, длина прямоугольника может свидетельствовать о продолжительности операции.
3. Разработка графика начинается с размещения на нем исходной работы в крайней левой точке и завершается включением в него конечной операции, закрывающей проект. Календарно начальный момент исходного действия обозначает старт проекта.
4. Зависимости (связи) между работами оформляются стрелками, направленными слева направо под разными углами наклона. На основе данного правила связи между операциями определяются одной из форм отношений зависимости.
5. Сетевой график имеет только одну работу, в которую входят зависимости, но не выходит ни одна, и одну работу, не имеющей ни одной входящей зависимости.
6. Сетевой график не может иметь циклов, т.е. зависимости не должны связывать работы по кругу.

Вид сетевого графика метода «вершина – работа»

Сетевой график строится по следующему алгоритму составления.

1. На диаграмме размещается начальная работа проекта, не имеющая предшественников.
2. Расположение операции, непосредственно следующей за работой, связанной с ней отношением предшествования, на графике левее предыдущей. Отображение связи предшествования.
3. Переход к пункту 2 до тех пор, пока не закончатся работы, имеющие предшественников.

Разработка сетевой диаграммы производится с учетом возможных связей между работами. Основные виды отношений предшествования используются в четырех вариантах связей и в двух дополнительных их разновидностях. Далее на схеме представлены варианты связи следующей по идентификационному номеру работы к предыдущей или, наоборот, последующей. Основные или базовые виды предшествования связаны с перестановками слов «начало» и «окончание»:

• «окончание – начало» (простой вид отношения предшествования);
• «окончание – окончание»;
• «начало – начало»;
• «начало – окончание».

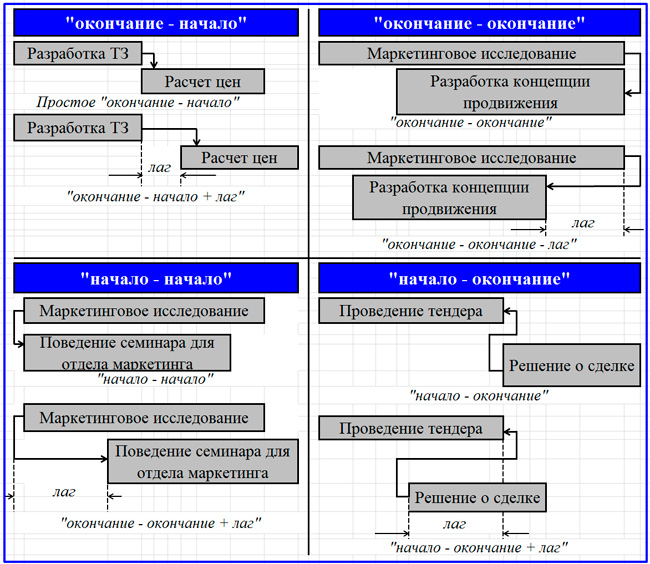Примеры вариантов отношений предшествования

Понятие «операция» в сетевом планировании

В сетевом графике можно оценить периоды начала (окончания) выполнения работ, вынужденные простои и, соответственно, максимальные сроки задержки производства тех или иных операций. Кроме того, выявляются критические операции – те, которые не могут выполняться с отклонением от графика.

Разбираясь с терминологией планирования, необходимо четко представлять себе, что такое операция. Чаще всего под этим понимают неделимую часть работ, требующую времени на выполнение. Далее мы понимаем, что с выполнением операции связаны затраты: времени и ресурсов (как трудовых, так и материальных).

В отдельных случаях для выполнения каких-то действий не нужны ресурсы, требуется только время, которое учитывает сетевой график. Пример этого — ожидание застывания бетона (в строительстве), время остывания прокатных деталей (металлургия) или же просто одобрение (подписание) контракта или разрешительной документации.

Чаще всего операциям в планировании дают наименование в повелительном наклонении (разработать спецификацию); иногда для названий используют отглагольные существительные (разработка спецификации).

Предварительный этап построения сетевого графика

На предварительном этапе сетевого планирования необходимо определить характер планируемых операций и потенциал сотрудников, которые будут отвечать за их выполнение.

В качестве примера возьмем работу регионального Агентства по молодежной политике на месяц и запланируем перечень операций на месяц.

Допустим, что количество сотрудников – 10 человек.

Типовая оргструктура Агентства по молодежной политике

Построение сетевого графика представляет собой элемент управленческой деятельности и соответствует общему процессу принятия решений. Это неотъемлемая составляющая процесса управления. В ходе построения сетевого графика рассматриваются несколько вариантов выполнения запланированных операций и в итоге выбирается наилучшая альтернатива из множества доступных. В сетевой график включаются непосредственно управленческие действия и операции, связанные с технической стороной деятельности организации.

Управленческие и технические операции в сетевом графике

Управленческие операции	Технические операции
Общее управление внутренними процессами в организации	Непосредственное проведение запланированных операций
Проектирование системы управления	Подведение итогов
Стратегическое планирование	Работа с документами, регистрами
Управленческое консультирование	Оценка результатов
Управление сотрудниками	Оформление документации
Взаимодействие с внешней средой	Формализация результатов

Операции в сетевом графике должны быть зафиксированы документально, например, в распорядительных документах. Основное назначение такой документации состоит в регулировании деятельности объекта управления, обеспечении его финансовыми, трудовыми, материальными и информационными ресурсами. Основные формы документального представления запланированных операций:

1. Приказы – в том числе распоряжения, указания;
2. Акты – в том числе акцепты и протоколы;
3. Договоры – в том числе, соглашения, контракты, оферты;
4. Регламенты – инструкции, положения, правила, планы, модели.

Метод сетевого моделирования

Сетевое планирование и управление получило активное развитие с 50-х годов прошлого века сначала в США, затем в других развитых странах и в СССР. Такие методы сетевого планирования, как CPM, PERT позволили существенно поднять «планку» проектного управления в направлении оптимизации временных и содержательных параметров графиков работ. Это дало возможность разрабатывать расписания проектных задач на основе более эффективной методологии сетевого моделирования, вобравшей в себя весь лучший опыт (схема методов календарного планирования приведена ниже). Сетевая диаграмма имеет различные названия, среди них:

• сетевой график;
• сетевая модель;
• сеть;
• граф сети;
• стрелочная диаграмма;
• PERT-диаграмма, и т.д.

Визуально сетевая модель проекта представляет собой графическую схему последовательного комплекса работ и связей между ними. Стоит заметить, что система планирования и управления проектом целостно отображается в графической форме состава операций, их временных протяженностей и взаимосвязанных событий. Основой метода построения модели служит раздел математики, именуемый теорией графов, сформировавшийся в начале 50-х – конце 60-х годов.

Методы календарного планирования и управления проектам

В модели сетевого планирования и управления под графом понимается геометрическая фигура, включающая бесконечное или конечное множество точек и линий, соединяющих между собой эти линии. Граничные точки графа называют его вершинами, а ориентированные в направлениях соединяющие их точки – ребрами или дугами. Сетевая модель в свой состав включает именно ориентированные графы.

Вид ориентированного графа

Разберем другие основные понятия сетевой модели проекта.

Работа – часть производственного или проектного процесса, имеющая начало и окончание в форме количественно описываемого результата, требующая затрат времени и других ресурсов. Работа отражается на диаграмме в форме однонаправленной стрелочной линии. Формой работ мы можем считать операции, мероприятия и действия.

Событие – факт завершения работ, результат которых необходим и достаточен для начала реализации следующих операций

Вид события на модели отражается в форме кружков, ромбиков (вехи) или других фигур, внутри которых помещается идентификационный номер события.

Веха представляет собой работу с нулевой продолжительностью и обозначает важное, значимое событие в проекте (например, утверждение или подписание документа, акт окончания или начала проектного этапа и т.п.).

Ожидание – это процедура, которая не потребляет никаких ресурсов, кроме затрат времени. Отображается как линия со стрелкой на конце с отметкой длительности и указанием наименования ожидания.

Фиктивная работа или зависимость – вид технологической и организационной связи работ, не требует никаких усилий и ресурсов, в том числе затрат времени

На сетевой диаграмме показывается как пунктирная стрелка.

Решение задач сетевого планирования

Срок выполнения	от 1 дня
Цена	от 100 руб./задача
Предоплата	50 %
Кто будет выполнять?	преподаватель или аспирант

УЗНАТЬ СТОИМОСТЬ РАБОТЫ ПО СЕТЕВОМУ ПЛАНИРОВАНИЮ

Решение задач сетевого планирования студенты изучают на различных дисциплинах, связанных с теорией графов и методами оптимального решения. В данной статье будут рассмотрены два примера решения таких задач. Мы постараемся не использовать сложных и запутанных формул, чтобы показать, как на самом деле всё просто.

Суть задачи

 Задачи сетевого планирования сводятся к двум целям:

1. Найти оптимальный маршрут;
2. Определить, как максимально быстро выполнить проект.

 В первом случае рассматриваются такие случаи, когда необходимо соединить несколько независимых узлов, находящихся в одной сети. Сделать это необходимо максимально коротким способом.

Например, в некотором районе города требуется провести трубопровод к нескольким домам. Понятно, что к разным домам могут вести несколько дорог.

Таким образом, нам нужно определить, какой из маршрутов прокладки будет наиболее коротким. Узлами в этом случае будут наши дома.

Во втором случае задачи предполагают, что существует некий проект, который состоит из нескольких работ. Работы могут выполняться поочередно, друг за другом, но не каждая из них для начала выполнения требует завершения какой-то из предыдущих работ.

Соответственно, обе задачи решаются с помощью графов – точек, соединенных между собой произвольными линиями.

В задаче первого типа граф даётся, как правило, условием задачи, а во втором случае его необходимо изобразить самостоятельно. Этим мы сейчас и займёмся.

Первый случай

  Выше вы видите граф. Цифры в кружках – это дома, к которым телевизионная компания планирует подвести кабеля. Как мы видим, к одному кружку могут вести два или три пути. Пути называются рёбрами графа. У каждого пути есть свой вес. Это наше расстояние.

Нам нужно выбрать из всего этого обилия путей самый короткий, который объединит каждый кружок – вершину графа. Для этой цели существует специальный алгоритм «Прима». Его суть заключается в следующем: Мы начинаем идти из первой вершины и присоединяем к ней ребро, имеющее самый маленький вес. В нашем случае – это ребро 1;2.

Его вес равен 1. Теперь мы присоединяем самое короткое ребро, из всех выходящих из вершин 1 и 2. Это ребро 2;5. Его вес – 3. У нас уже три вершины – 1,2,5. Присоединяем самое короткое ребро, выходящее из них. И это – 2;4. Его вес – 4. Самое короткое ребро, выходящее из вершин 1,2,4,5 – 4;6. Оно равно 3. Последнее ребро – 4;3.

Мы объединили все вершины. Наш путь в сумме составляет: 1 + 3 + 4 + 3 + 5 = 16.  

Второй случай

 Здесь всё немного сложнее, чем в вышеописанном примере. По условию даётся таблица примерно следующего характера.   На основании данной таблицы мы рисуем следующий граф.

  Правила при составлении графа простые: Каждая следующая работа всегда находится правее предшествующей. 

Никакая работа не может быть начата без выполнения всех предыдущих по условию.

Мы не могли бы начать делать b10, не сделав b3, выполнение которой приходится на вершину 3. Мы не можем строить стены, не возведя фундамент.

Тупиков быть не должно. Из каждой вершины выходит как минимум, одно ребро. Далее мы находим так называемый «критический путь». Это самое длинное расстояние от 0 до 6. Мы начинаем двигаться из нуля и присоединяем каждую вершину самым длинным путём. Например, 3 мы можем присоединить, пройдя ребро 0;3, вес которого – 8 или два ребра – 0;1 и 1;3, а так же 0;2 и 2;3.

Обратите внимание, что ребро 3;5 имеет нулевой вес, поэтому и кратчайший путь к вершине 3 будет равен 12. Подпишем самые короткие пути снизу вершин

  Там, где разница между самым коротким и самым длинным путём будет равна нулю, проходит критический путь. На рисунке ниже он подчёркнут двойными чертами.   

Это крайний срок выполнения проекта. Он равен 3 + 9 + 7 = 19.

Раньше этого успеть нельзя. По остальным работам есть резерв времени. Чтобы его посчитать, отнимите верхнее число от нижнего над каждой вершиной.

Что это?

Одной из методик эффективного планирования деятельности производственного предприятия является построение сетевого графика. Изначально он использовался в строительстве и определял не столько последовательность работ, сколько сроки выхода на строительную площадку бригад рабочих разных специальностей. Он называется «календарный план выполнения работ».

В современных условиях, когда крупные предприятия массово выпускают продукцию, для облегчения и повышения производительности весь процесс разбивается на простые операции. Поэтому сетевой график «перекочевал» из строительства практически во все отрасли.

Итак, что же отображается в этом документе? Во-первых, подробнейшим образом перечисляются все операции, необходимые для выпуска товаров (производства услуг). Во-вторых, определяется логическая взаимозависимость между ними. И, наконец, в-третьих, рассчитываются не только сроки выполнения каждой конкретной работы, но и время, необходимое для полного завершения производственного процесса.

Раскрывая внутренние зависимости операций проекта, сетевой график становится базой для календарного планирования загруженности оборудования и рабочей силы.

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

Таблица операций для построения сетевого графика

Номер операции	Предыдущие операции	Кол-во исполнителей, чел.	Продолжительность, дни
1.	—	10	1
2.	1	2	3
3.	1	3	1
4.	1	2	4
5.	4	1	0,5
6.	3	3	2
7.	5	2	0,5
8.	2,7,6	10	0,5
9.	9	10	0,5
10.	9	1	3
11.	9	2	4
12.	9	2	2
13.	9	2	3
14.	12	2	2
15.	13	3	2
16.	10,11,14,15	10	0,5
17.	16	10	0,5
18.	17	2	2
19.	18	2	3
20.	17	2	2
21.	17	2	3
22.	21	3	1
23.	20	2	2
24.	19,22,23	10	0,5
25.	24	10	0,5
26.	25	5	1
27.	26	5	3
28.	25	3	2
29.	28	3	2
30.	25	2	4
31.	27,29,30	10	0,5
32.	31	10	0,5
33.	32	7	1
34.	32	2	1
35.	33,34	10	1

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Метод сетевой модели номер два

Вторым методом сетевого планирования, по праву завоевавшим популярность среди проект-менеджеров, является диаграмма, называемая «вершина – работа». В англоязычной версии модель сокращенно обозначается как AoN (Activity on Node). Метод отличается большей простой и наглядностью, предлагает узлами модели делать не события, а работы. При этом длина прямоугольников, обозначающих операции, может указывать на их длительность во времени. Отношения предшествования между ними оформляются прямыми или фигурными стрелками.

Такую диаграмму сформировать значительно проще, чем AoA. Тем не менее, алгоритм работы над ней очень похож. События на диаграмме не размещаются, но они предполагаются в завершении каждой работы. Помимо прочего, событиям все-таки уготовано место на сетевом графике, но в форме особых фактов, именуемых вехами. Веха – это особенное значимое событие проекта, и не каждая операция должна ею завершаться. Поэтому диаграмма может быть разгружена от несущественных событий, но отражать важные, ключевые моменты проектной реализации.

Пример сетевой диаграммы метода «вершина – работа»

Если воспользоваться возможностью вариации длины прямоугольников работ, превращая их в ленты, размер которых соответствует длительности реализации, то сетевой график превращается в диаграмму Ганта. Диаграмма вида AoN при этом становится похожей на АоА. В методе AoN отпадает необходимость в изображении фиктивных работ, требуемых в модели «ребро – работа» для своеобразной «упаковки» событий. Благодаря этому лишние, искусственные сущности исключаются из поля зрения менеджера проекта. Вехи в этом отношении являются более интересным решением, располагаясь, как и все работы, в узлах сетевого графика.

Работы перестают выполнять двойную функцию связующих события элементов и непосредственного обозначения выполняемых операций. Для метода AoN не требуется нумерации, что дает PM мобильность для свободного маневрирования числом мероприятий. И в этом кроется еще одно удобство метода «вершина – работа». В сетевой диаграмме должны быть учтены возможности применения различных связей предшествования. Их количество не столь велико, как может показаться на первый взгляд. Оно связано с вариантом связи предшествования и с эффектом отставания или опережения в отношении к примененной типовой связи. Все это мы рассмотрим в отдельном материале, посвященном практике сетевого планирования и управления.

В настоящей статье мы рассмотрели методы сетевого планирования и управления. В современной проектной практике отдается предпочтение методу AoN как более доступному и наглядному. Это не означает, что метод АоА плох, многие специалисты, освоив его, с успехом применяют. Обе модели приводят к одному и тому же результату, но с двух взаимосвязанных сторон: работ и событий. Проект-менеджер должен понимать суть и уметь применять каждый из представленных инструментов. Это связано с тем, что задача сетевого планирования состоит в поиске наиболее экономичных, ясных решений построения событийной и временной последовательности в условиях ограничений.

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с , для этого нужно снять отметку с пункта Нумерация вершин с №1.

12341103015
Нумерация вершин с 0
1231103015

Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.

docxpngMicrosoft Visioduration, ES, EF, LS, LF, and slack

Автоматическая сетевая диаграмма проекта с критическим путем в EXCEL

Построим автоматическую сетевую диаграмму проекта. Сетевую диаграмму изобразим на диаграмме MS EXCEL типа Точечная. На этой диаграмме выведем работы проекта в виде точек, стрелками изобразим связи между работами. Также изобразим на диаграмме критический(ие) путь(и). Сетевая диаграмма будет автоматически перестраиваться при изменении связей между работами и их длительности.

Данная статья является третьей статьей в цикле статей посвященных построению сетевой диаграммы проекта и является синтезом первых двух:

1. В статье Метод критического пути в MS EXCEL показано как рассчитать длительность проекта, определить работы на критическом пути и как построить сетевую диаграмму проекта на листе MS EXCEL. Основной недостаток – при изменении связей между работами пользователю потребуется вносить серьезное изменение в сетевую диаграмму.
2. В статье Автоматическая сетевая диаграмма проекта в MS EXCEL показано, как имея перечень работ и связи между ними, вычислить все пути проекта и отобразить их на стандартной диаграмме типа Точечная. При изменении связей – пути автоматически пересчитываются. Однако, критический путь не вычислялся в этой статье.

Рекомендуется прочитать вышеуказанные статьи перед первым прочтением.

Ниже показана диаграмма, которую мы будем создавать в этой статье. На диаграмме отображены все работы проекта (от А до U, синие точки), связи между ними (стрелки), работы на критическом пути (красные точки), критический путь (красные стрелки).

Примечание : Слово диаграмма используется в 2-х смыслах: сетевая диаграмма проекта (стандартный термин из управления проектом, Activity-on-node diagram ) и диаграмма MS EXCEL ( Excel Chart , см. вкладку , группа ). Диаграмма MS EXCEL типа Точечная будет использоваться для построения сетевой диаграммы проекта.

При изменении связей между работами и/или их длительности происходит перерасчет критического пути и сетевая диаграмма автоматически обновляется. Например, значительное увеличение длительности работы М (в нижнем пути сетевой диаграммы) приведет к изменению критического пути.

Такая сетевая диаграмма отображает критический путь даже нагляднее, чем стандартная диаграмма Ганта , хотя, конечно, не заменяет ее.

ВНИМАНИЕ! Построение данной сетевой диаграммы в этой статье приведено лишь с целью демонстрации технической реализуемости такого построения в MS EXCEL. Не ставилось целью сделать “удобную программу для пользователей”

Это означает, что при изменении пользователем количества работ/ добавления связей между работами (например, использования более 5 последователей), переименовании листов, рядов диаграммы и других изменений, в файле примера может потребоваться дополнительная настройка формул.

Такая настройка потребует от пользователя серьезных знаний MS EXCEL и времени.

Исходная информация

В качестве исходной информации дан перечень работ, их длительность и связи между работами.

Также вручную задаются координаты для отображения на диаграмме работ (диапазон ВА12:ВВ34 ).

Другой информации для построения сетевой диаграммы и вычисления критического пути не требуется.

Вычисление путей сетевой диаграммы

Как и в статье Автоматическая сетевая диаграмма проекта в MS EXCEL начнем построение сетевой диаграммы с вычисления путей.

В отличие от указанной статьи, здесь увеличено количество рассчитываемых путей (до 15) и максимальная длина путей (до 10 работ, включая вехи начала и окончания).

Алгоритм вычисления путей аналогичен, однако формулы изменены, чтобы позволить пользователю быстро увеличивать количество путей проекта и их длину.

Начиная с шага №1 (начиная со строки 96) формулы можно копировать вниз и вправо, чтобы при необходимости увеличить количество путей и их длину (количество шагов). На каждом шаге длина путей увеличиваются на одну работу. В случае наличия нескольких последователей у работы – увеличивается количество возможных путей.

После вычисления всех шагов, в диапазоне R62:AA76 выводится перечень всех путей проекта, содержащие входящие в них работы.

Построение сетевой диаграммы

Сначала на диаграмме выводятся работы (синие точки, ряд Работы ).

Затем выводятся все возможные пути проекта (ряды Путь_1, Путь_2, …, Путь_15 ).

Все работы, находящиеся на критическом пути, отмечаются красным цветом. Также на диаграмму выводится критический путь. Если путей несколько, то выводятся все пути (в файле примера выводятся максимум 3 критических пути). Если длительность работы О увеличить до 8 дней, то 3 пути станут критическими с длительностью по 65 дней.

Одновременно, работы проекта отображаются на диаграмме Ганта.

Методы оптимизации сетевого графика

сетевыми моделями
Для возможности оптимизации сетевой модели, все исходные данные вводятся в виде таблицы (Операции/Добавить в виде таблицы).

• Оптимизация сетевой модели по критерию «число исполнителей». Заполняется столбец Количество исполнителей Ч ►
• Оптимизация сетевой модели по критерию «время – стоимость» (время — затраты). В случае известных коэффициентов затрат на ускорение работ заполняется только этот столбец h(i,j). Иначе, заполняются столбцы t_опт (Нормальный режим), Минимальное время работ, t_min (Ускоренный режим), Нормальная стоимость, Cн и Срочная стоимость, Cc.

Графики привязки (а) и загрузки (b) до оптимизации

1,261,311,452,532,613,684,644,725,866,817,8311223194175678189101112131413151617181019202122423242526127

Графики привязки (а) и загрузки (b) после оптимизации

1,261,311,452,532,613,684,644,725,866,817,831122311414567158910111812131415101617184192021221023242526727